¿Qué hace hoy un matemático?

Parte 1


Parte 2

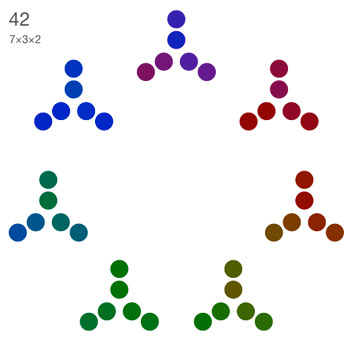
Factorizando números visualmente

Esta preciosa e ingeniosa forma de visualizar los factores de los diferentes números es una maravilla

http://www.datapointed.net/visualizations/math/factorization/animated-diagrams/

“D”… terror sobre el libro de geometría

En una oscura y antigua biblioteca, un libro de geometría permanece abierto sobre una gran mesa. En una de sus páginas hay un ejercicio que consiste en cuatro puntos geométricos, A, B, C y D, que deben ser unidos por una linea de tinta. Sobre esa misma mesa, una pluma fuente duerme y ronca hasta que un trueno la despierta...


http://ztfnews.wordpress.com/2012/04/23/d-terror-sobre-el-libro-de-geometria/

Horizontes Matemática

Todos los videos de Horizontes Matemática a tu alcance en una sola página

Horizontes Matemática | Conectate

Inspirations - Cristóbal Vila (2012)

Este vídeo resume de manera breve y magistral algunos hitos esenciales de la historia de las Matemáticas...Desarrollos planos cerrándose para formar poliedros; el poder de la duplicación (potencias de 2) en el famoso problema de los granos de trigo sobre las casillas de un tablero de ajedrez; El problema de los siete puentes de Konigsberg (Euler); mosaicos y partición regular de la superficie; trazado de una curva cicloide a partir de un punto fijo en una circunferencia (rueda) que gira; la belleza sintética de algunas fórmulas matemáticas esenciales (teorema de Fermat,…); la historia de la Matemática a través de los retratos de matemáticos ilustres; el aparato de Galton (o binostato) para el estudio empírico de modelos probabilísticos; el mundo “matemágico” de Mauritius Cornelius Escher; pentominós, juegos y puzzles planos y tridimensionales; estructuras mecánicas de Leonardo da Vinci; los fractales en la naturaleza; la geometría en los objetos cotidianos…

Los 10 números más importantes en el mundo

¿Eres de los que piensan que los números son importantes solamente dentro de las Matemáticas? Pues te equivocas, y hay multitud de ejemplos que lo confirman. Por ejemplo, en este vídeo se muestran (para los autores) los diez números más importantes del mundo y se cita algún lugar donde cada uno de ellos tiene esa importancia. Los números elegidos son los siguientes: El número de Avogadro. La constante de Hubble. El número de Euler e. La constante de Planck. La unidad imaginaria i. La proporción áurea. La constante de gravitación. La constante de Boltzmann. Pi. La velocidad de la luz.

Historia de las Matemáticas

Contenidos Educativos Digitales

Excelente link con contenidos interactivos
http://conteni2.educarex.es/?c=11

¿Cómo son los números reales?

¿Cómo se clasifican los números?


¿Cómo son los números naturales?


¿Cómo son los números enteros?


¿Cómo son los números racionales?


Fracción generatriz


Suma y resta de fracciones

http://educacion.practicopedia.lainformacion.com/matematicas

Criba de Eratóstenes animada

La criba de Eratóstenes es el método más antiguo para obtener una lista de los números primos: consiste básicamente en ir tachando primero los múltiplos de 2, luego de 3, luego de 5, etcétera empezando en cada ronda con el primer número que queda sin tachar (que se considera primo) y siguiendo afanosamente con todos sus múltiplos.

Este vídeo muestra visualmente cómo actúa el algoritmo con un color para cada número: las diferentes curvas van tocando la recta de los números enteros en puntos que son los diferentes múltiplos. Los valores que sobreviven a la criba son los números primos.

Diagramas de Voronoi en un campo de fútbol

http://www.geogebratube.org/student/m39116

Ábaco

Ábaco es una palabra Latina que tiene sus orígenes en la palabra Griega abax o abakon (significando "tabla" o "tablilla") las cuales se transformaron, originadas posiblemente desde la palabra Semita abq, significando "arena".
Vean todo lo que hacen estos niños japoneses 

Sistemas de 3 ecuaciones

Interesante herramienta para resolver sistemas de tres ecuaciones con tres incógnitas, como por ejemplo:

3x + 2y - z = 8

4x - 3y + 2z = 5

x + 3y + 2z = 3

Sistemas de 3 ecuaciones

“Algebra versus Cockroaches”

Aprende funciones lineales para matar cucarachas

“Algebra vs Cockroaches” es un juego en el que se necesita tener conocimientos básicos de funciones lineales. Se puede elegir un tipo de arma para destruir las cucarachas que se desplazan en línea recta sobre el eje de coordenadas. El objetivo es determinar la ecuación lineal sobre la que se mueven las cucarachas.

Cada cierto tiempo aparecerán más bichos, y se pierde cuando aparece la 16° cucaracha.

En el apartado instrucciones nos enseña, con un ejemplo, la forma de calcular la pendiente y la ordenada en el origen, y también qué coeficiente de la ecuación representa cada una.

Destacar por último que hay varias rondas en el juego con dificultad creciente; por ejemplo en la primera sólo aparecen funciones constantes, en la segunda sólo funciones que pasan por el origen, etc.

Se puede guardar el juego, para que la próxima vez que se inicie lo haga por la ronda que se había alcanzado.

http://mate.maticas.com/educacion/aprende-funciones-lineales-para-matar-cucarachas-y-mas/