Matrices 1

¡Matemáticas para rato!

Aquí te dejo algunos sitios en los cuales puedes encontrar recursos matemáticos para aprender jugando, para todas las edades:

Las Aventuras del Señor π. Realizando operaciones matemáticas básicas en el menor tiempo posible, ayudarás a este superhéroe a terminar con los malvados planes de Malasombra.
http://www.supersaber.com/espacioMultiplica.htm
http://www.supersaber.com/carreraSumaResta.htm

Metamáticas con Mario. Este simpático cocinero tiene una sorpresa para ti. Pero primero ¡a calcular!
http://www.educa.jcyl.es/educacyl/cm/zonaalumnos/tkPopUp?pgseed=1172775298308&idContent=8940&locale=es_ES&textOnly=false

El pastor, la oveja y el lobo. Pensando lógicamente, debes lograr que el pastor pase la oveja, el lobo y el cajón de vegetales al otro lado del río. Pero... ¡Cuidado! No puedes dejar al lobo a solas con la oveja, ni a la oveja a solas con el cajón de vegetales.
http://www.matematicasbachiller.com/juegos/pastor.html

Multiplicar, multiplicar, multiplicar. Organizados por niveles, una amplia variedad de cálculos para practicar las tablas de multiplicar.
http://www.educalandia.net/multiplicar/index.php

Adivina el número. Tu capacidad para estimar y una serie de sugerencias te ayudarán a descubrir un número del 1 al 100.
http://genmagic.org/menuprogram/mates1/pn1c.html

Sudoku. Partiendo de algunos números ya dispuestos en algunas de las celdas, debes rellenar una cuadrícula de 81 casillas, dividida en subcuadrículas con las cifras del 1 al 9. ¡Mucha paciencia y dotes lógicas!
http://www.matematicasbachiller.com/juegos/sudoku/sudoku.html

Tangram. Diviértete jugando y poniendo en práctica los principios de traslación, rotación y simetría. ¿Eres capaz de formar siluetas de figuras con las siete piezas dadas sin solaparlas?
http://www.redestudiantilpr.net/tangram1.htm

Tomado de http://www.docentesinnovadores.net/uncontenido.asp?id=714

Programación Lineal

Buscando algo del tema encontré este simpático video, recomendable

Simplemente números.

Número abstracto: El que no se refiere a una unidad de especie determinada.
Números amigos: Par de números enteros positivos tales que la suma de los divisores positivos de cada número menores que él es igual al otro número.
Número cardinal: Cada uno de los enteros considerados en abstracto.
Número complejo: Número de la forma a + bi con a y b, números reales e i2 = -1.
Número compuesto: El que se expresa con dos o más guarismos. Número que no es primo (excepto el uno).
Número concreto: El que expresa cantidad de especie determinada.
Número congruente: Cada uno de los miembros de un par de enteros que, divididos por un tercero llamado módulo, dan restos iguales.
Número cósico: Número que es potencia exacta de otro.
Número e: Número irracional transcendente que puede obtenerse como límite de la sucesión: (1 + 1/n )n cuando n tiende a infinito.
Número de Fermat: Todo número de la forma 22n+1; para cada n = 1,2,3, .....
Número deficiente: El que es inferior a la suma de sus partes alícuotas.
Número dígito: El que puede expresarse con un solo guarismo. 0, 1, 2, 3, 4, 5, 6, 7, 8, 9.
Número entero: El que consta exclusivamente de una o más unidades, por oposición a los quebrados y los mixtos.
Número Factorial: Es el producto de números consecutivos naturales
n! = (n)·(n-1)·(n-2)·.........3·2·1
En esta expresión se define que 0! = 1 y que 1! = 1.
Número fraccionario (o quebrado): Número que expresa una o varias partes de la unidad.
Número imaginario: Número que resulta de extraer la raíz cuadrada de un número negativo. Número impar: Número que no es divisible exactamente por dos.
Número mixto: Número compuesto de entero y fracción.
Número negativo: Número menor que 0.
Número ordinal: el que expresa idea de orden o sucesión.
Número par: Número divisible exactamente por dos.
Número perfecto: Número entero y positivo igual a la suma de sus divisores positivos, excluido él mismo.
Números pitagóricos: Ternas de números enteros positivos tales que el cuadrado de uno de ellos es igual a la suma de los cuadrados de los otros dos. Si las longitudes de los dos lados de un triángulo son enteros y pitagóricos, el triángulo es rectángulo.
Número plano: Número que procede de la multiplicación de dos enteros.
Número poligonal: Número natural de la sucesión n0 = 1, n1 .. nr ..., en la que nr = nr-1 + (m-2)r +1, donde m es un número natural mayor que dos. Para m = 3,4,5... se obtienen los números triangulares, cuadrangulares, pentagonales... El número nr es el de los puntos marcados en un esquema geométrico formado con triángulos, cuadrados, pentágonos..., respectivamente.
Número positivo: Número mayor que 0.
Número primo: El que sólo es exactamente divisible por sí mismo y por la unidad. Los primeros son: 2, 3, 5, 7, 11, 13, 17, 19, ...
Número rectangular: Que se puede disponer, en base a figuras, en forma de rectángulo.
Número sólido: Número obtenido de la multiplicación de tres enteros.
Número sordo: Número que no tiene raíz exacta.
Número superante: Número que es superior a la suma de sus partes alícuotas.
Número transfinito: Número cardinal que no es entero.
Número trascendente: Número que no es raíz de ninguna ecuación algebraica con coeficientes racionales.
Número triangular: Número natural de la sucesión n0 = 1, n1 ... nr ..., en la que nr = nr-1 + r +1,... El número nr es el de los puntos marcados en un esquema geométrico formado con triángulos.

Tomado de http://www.sectormatematica.cl/

Matematicas de Microsoft 2009 Calculadora

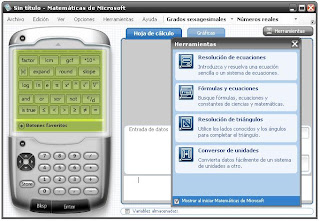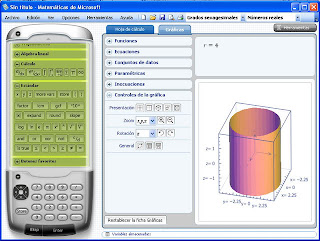
Portable Matemáticas de Microsoft 2009 es un conjunto de herramientas matemáticas que puede ayudarte a que tu trabajo sea más rápido y sencillo. Lo más destacado de Matemáticas de Microsoft es una compleja calculadora científica con amplias capacidades de representación gráfica y de resolución de ecuaciones. Puedes utilizarla como una calculadora de mano, pulsando sus botones, o también puedes usar su teclado para escribir aquellas expresiones matemáticas que quieras que la calculadora evalúe.

Es una excelente calculadora gráfica en dos y tres dimensiones.
El trabajo puede guardarse a la mitad para terminar más tarde, añadirse a documentos Word o PowerPoint o compartido entre grupos de estudio.

Lo mas importante que por ser Portable la puedes llevar donde quieras en tu USB, nada se instala en tu equipo.

Microsoft Student viene con una calculadora gráfica en dos y tres dimensiones, plenamente funcional y de fácil manejo.

Entre otros componentes de Matemáticas de Microsoft podemos incluir:

* Resolución de ecuaciones paso a paso.
* Apuntes de matemáticas.
* Resolución de triángulos.
* Fórmulas y ecuaciones.
* Conversor de unidades.

La calculadora gráfica también ofrece:
* Herramientas para convertir fórmulas cientí­ficas y ecuaciones matemáticas
en gráficas, desde las matemáticas más simples al cálculo infinitesimal.
* Tecnologí­a tridimensional.
* Aspecto externo personalizable.

Resolución de triángulos.
Este instrumento desarrolla capacidades de geometrí­a. Ahora los estudiantes pueden introducir fácilmente sus propios valores.

La calculadora:
* Determina la información desconocida.
* Dibuja el triángulo a escala.
* Provee las reglas matemáticas usadas para calcular los valores que faltan.

Conversor de unidades.
Esta herramienta resulta sumamente útil tanto en matemáticas como en ciencias al facilitar a los estudiantes la rápida conversión de unas unidades de medida a otras en magnitudes como:

* Longitud.
* Area.
* Volumen.
* Peso.
* Temperatura.
* Presión.
* Energí­a.
* Potencia.
* Velocidad.
* Masa.

Descargala aquí:
http://www.mediafire.com/download.php?xqztwjytz4z
http://www.megaupload.com/?d=2AMKIHRJ
http://rapidshare.com/files/155614504/Portable_Matem_ticas_de_Microsoft_2009_by_hleon.rar.html


Tomado de:http://bloghost.cl/bernardobello/2009/09/05/matematicas-de-microsoft-2009-calculadora/

Gráfica de funciones

Open publication - Free publishing - More math

El rostro humano de las matemáticas

Interesante listado de lecturas con mucho contenido matemático

Open publication - Free publishing - More math

Belleza y las matemáticas

Belleza Y Las Matemáticas - For more amazing video clips, click here

Matemáticas secretas (Criptografía)

La criptografía es el arte o ciencia de cifrar y descifrar información mediante técnicas especiales y es empleada frecuentemente para permitir un intercambio de mensajes que sólo puedan ser leídos por personas a las que van dirigidos y que poseen los medios para descifrarlos. Su finalidad es, en primer lugar, garantizar el secreto en la comunicación entre dos entidades (personas, organizaciones, etc.) y, en segundo lugar, asegurar que la información que se envía es auténtica en un doble sentido: que el remitente sea realmente quien dice ser y que el contenido del mensaje enviado, habitualmente denominado criptograma, no haya sido modificado en su tránsito.

Cómic sobre las matemáticas en Egipto

Historia de las Matemáticas (en Cómic).
JOSÉ LUIS CARLAVILLA y GABRIEL FERNÁNDEZ. PROYECTO SUR DE EDICIONES

Láminas de Lolita Brain

Excelente material, vale la pena mirarlo.

Open publication - Free publishing - More revistas

La rebelión de los ceros (II)

IV

La asamblea bullía entre la trascendencia de las quejas presentadas por el cero y el uno, y el riesgo que implicaría un paro, una huelga o simplemente el tortuguismo de parte de estos dos importantes dígitos, ya que esto representaría desde un mal funcionamiento de todo el sistema internacional de cómputo y comunicación, hasta su total paralización cuyas repercusiones serían de consecuencias imprevisibles.

V

En una mesa de nivel superior a la de los dígitos, frente a la asamblea se encuentra el presidium integrado por tres números que recientemente han sido elegidos como dirigentes del máximo tribunal: Al centro preside el número pi que aun cuando forma parte del sedicioso grupo de los números irracionales, se le ha reconocido por su carácter hermético, por pertenecer al pequeño y exclusivo círculo de los trascendentes, pues cuenta con una esfera muy amplia de conocimientos, y por ello se le augura un éxito rotundo. A la derecha del número pi se encuentra el número e ,otro número irracional, que cuenta con gran influencia yreconocimiento puesto que es la base de los logaritmos naturales. El número e se siente muy orgulloso de su origen exponencial, puesto que procede de una serie infinita y todos los asambleístas reconocen su enorme valor, aún cuando éste se exprese en forma decimal. Finalmente, fungiendo como secretario, se encuentra, a la izquierda, el número i, como representante del sector radical; dueño de una compleja capacidad imaginativa, se le tiene confianza porque su radicalismo se elimina simplemente con elevarlo al cuadrado y su valor queda reducido a una unidad negativa.

VI

Los números naturales ocupan, como de costumbre, el ala derecha de la asamblea y están preocupados por el impacto ecológico y las consecuencias que pueda ocasionar la posición intransigente del cero y el uno. En el ala izquierda de la asamblea, se encuentran los números irracionales, que personifican el área más incoherente, desequilibrada y difícil de manejar.
Con su densidad llegan a superar al conjunto de los enteros positivos, aun cuando éstos han ogrado duplicar su representación gracias a su reciente coalición con sus pares negativos.
En el centro de la sala se encuentran los racionales, aunque muy numerosos y densos, en todos ellos se pueden apreciar divisiones que afectan a la cohesión de su conjunto. Al fondo del salón, se ubican los números imaginarios, obscuros y taciturnos; casi todos están de acuerdo en que son
complejos y difíciles de comprender por su posición radical.
Casualmente no respondieron a la convocatoria los números aleatorios, lo cual no extrañó a la asamblea, ya que todos están de acuerdo en que estos números son impredecibles, además se sabe que han llevado una vida muy azarosa debido a su compulsiva propensión a los juegos de azar y a la especulación.

VII

La asamblea, sin duda muy numerosa, se desarrolló con un sinnúmero de incidentes -trascendentes algunos, irracionales otros-, se hicieron patentes las divisiones y las distintas fracciones, pero al final se votaron y aprobaron los siguientes acuerdos:
1. Se hace un reconocimiento universal por su importante participación en la modernidad a los incomprendidos y menospreciados ceros.
2. Se propondrá, que en las prácticas y transacciones comerciales se anote una simple rayita después del punto decimal para indicar que no hay centavos.
3. Se pedirá a los usuarios de computadoras que en adelante tachen a las oes (o) para no confundirlas con los ceros (0).
4. Finalmente, respecto a la solicitud de eliminar la prohibición de la división entre cero, no se pudo ni siquiera considerar, por la infinidad de consecuencias que esta decisión implicaría.

Benjamín de la Cueva G.

La rebelión de los ceros (I)

I

La asamblea de los números fue convocada por una querella planteada por los ceros.
No hay duda que los ceros han sido más abstractos, abstrusos y reservados que el resto de sus compañeros, los nueve dígitos; pero ahora su inconformidad ha llegado al clímax por la forma en que se les trata, y presentaron una queja al más alto tribunal de los guarismos que se concreta en los siguientes puntos:
1. Los ceros desde tiempos inmemoriales han sido calificados como inútiles: ”fulanito es un cero a la izquierda“, se dice en tono despectivo.
2. Los ceros demandan igualdad de trato pues no les hace ninguna gracia que pongan dos de ellos a la derecha del punto decimal nada más para indicar que no hay centavos.
3. Para numerar se empieza siempre con el uno, cuando el cero es el primero de los dígitos, sin duda alguna.
4. Con la introducción del lenguaje de computación se ha dado en tachar a los ceros ”0“ para distinguirlos de la letra O.
5. Finalmente, y ésta es la demanda de más fondo, no aceptan la limitación, que a través de todos los tiempos ha habido, de no permitir la división entre cero.
Todas las anteriores restricciones y discriminaciones van paralelas al aumento de las cargas de trabajo, para lo cual los ceros se han solidarizado con los unos, pues desde que se generalizó el uso de las computadoras que utilizan el sistema binario, la tarea, que anteriormente se distribuía uniformemente entre los diez dígitos, ahora debe ser soportada sólo por estos dos números, y el trabajo para ellos ha sido verdaderamente abrumador.

II

La importancia de los números nadie puede ignorarla, están íntimamente ligados a nuestra vida; desde el momento de nacer se nos pone una pulserita con un número para fines de identificación, son utilizados lo mismo para manejar las estadísticas demográficas de un país, que para reconocer las páginas de un libro; sirven para calcular la fecha y la hora de un eclipse o para medir el rendimiento escolar de un alumno.
Son usados tanto para determinar la deuda de una empresa, como para especificar las coordenadas de nuestra tumba. Sí, los números se encuentran por todas partes, proliferan más que los insectos, bacterias o esporas, se encuentran agazapados dentro de las computadoras, viajan encriptados o libremente vía módem por líneas telefónicas, fibras ópticas o por el espacio, brincando alegremente de satélite en satélite, circulando a lo largo y a lo ancho del planeta, conteniendo imágenes, sonidos, gráficas, y desde luego cifras que se codifican y decodifican automáticamente, fuera de nuestro control.

III

Al frente de una pletórica y ruidosa asamblea, sentados en una mesa rectangular se encuentran, colocados en riguroso orden creciente, de izquierda a derecha, los dígitos; muy orgullosos de poder representar por sí mismos a cualquier número entero o fraccionario sin importar qué tan grande sea.
Se puede apreciar en la mesa que está presente el nepotismo, ya que varios de sus integrantes son primos: el dos, el tres, el cinco y el siete. Fuera de este grupo, el cuatro, el seis, el ocho y el nueve son más liberales, ya que se dejan dividir, sin ningún recato, por otros números, aparte del uno, diferenciándose así de los exclusivos primos.
El cero se encuentra sentado en el extremo izquierdo de la mesa y es el único dígito adyacente a los números negativos, lo que probablemente justifique su cerrada y negativa forma de razonar.
Por otra parte, el cero es el más joven de la mesa, pues se le incluyó apenas en el siglo XII, cuando se estableció el uso de los números indo-arábigos, ya que hasta ese momento los números romanos, que no conocían el cero, gozaban de gran influencia y dominaban con sólo siete letras el panorama numérico en forma exclusiva.
Algunos tildan al cero de advenedizo, pues según se sabe, los mayas lo descubrieron desde los principios de la era cristiana.

¿Qué día del año cae Semana Santa?

Quizás muchas personas sientan la curiosidad de cómo se calcula la fecha en que se celebrará semana santa. Hoy decidí averiguarlo y grande fue mi sorpresa al descubrir que Carl Friedrich Gauss había estudiado este tema.

Según Gauss, para deducir cada año cuando ha de ser la Semana Santa, se toma el año que interese, al que llamamos N y se calculan los restos sucesivos por los números 19, 4 y 7. Después, se llevan esos valores obtenidos a las fórmulas siguientes, calculando nuevos restos.
Con todos ellos, se obtiene la fecha de la Semana Santa, calculando la expresión final. Repetimos pues que llamamos a, b y c a los primeros restos, es decir a = N / 19 (el resto), b = N / 4 (el resto) y c = N / 7 (el resto). Y ahora calculamos los valores d y e que son los nuevos restos de las expresiones siguientes: d = (m + 19 . a) / 30 (el resto) y e = (n + 2 . b + 4 . c + 6 . d) / 7 (el resto). Los valores de m y n se toman de la siguiente tabla:

Años	m	n
1583 - 1699	22	2
1700 - 1799	23	3
1800 - 1899	23	4
1900 - 2099	24	5
2100 - 2199	24	6
2200 - 2299	25	0

Finalmente si d + e < 10 Pascua será el (d + e + 22) de Marzo sino es el (d + e − 9) de Abril.
Debe tomarse en cuenta dos excepciones: Si la fecha resultante es el 26 de Abril, Pascua será el 19 de Abril.Si la fecha resultante es 25 de Abril, con d = 28, e = 6, y a > 10, Pascua es el 18 de Abril.

Para que puedas comprobar lo que hemos explicado, ponemos los valores que se obtienen para este año 2 009.
Los restos son: a = 14, b = 1, c = 0, d = 20, e = 1
Y con todos ellos se obtiene como fecha de la Pascua, el día 20 + 1 – 9 = 12 de abril.

Herramientas para el estudio de funciones gráficas

*GeoGebra

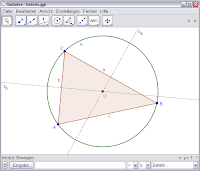GeoGebra es un programa interactivo especialmente diseñado para la enseñanza y aprendizaje de Álgebra y Geometría a nivel escolar medio (secundaria).
Por un lado, GeoGebra es un sistema de geometría dinámica. Permite realizar construcciones tanto con puntos, vectores, segmentos, rectas, secciones cónicas como con funciones que a posteriori pueden modificarse dinámicamente.
Por otra parte, se pueden ingresar ecuaciones y coordenadas directamente. Así, GeoGebra tiene la potencia de manejar con variables vinculadas a números, vectores y puntos; permite hallar derivadas e integrales de funciones y ofrece un repertorio de comandos propios del análisis matemático, para identificar puntos singulares de una función, como Raíces o Extremos.
Estas dos perspectivas caracterizan a GeoGebra: una expresión en la ventana algebraica se corresponde con un objeto en la ventana geométrica y viceversa.

Descargar GeoGebra

*Winplot

Winplot es un generador de funciones gráficas especialmente diseñado para el estudio visual de una serie de ecuaciones matemáticas.
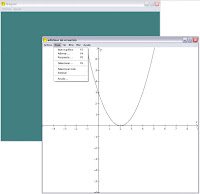
Concretamente, con Winplot puedes generar gráficas de ecuaciones explícitas, paramétricas, implícitas y cilíndricas, generar curvas simples, tubos e incluso representar ecuaciones diferenciales tanto en dos como en tres ejes (2D y 3D).
Obviamente, Winplot permite personalizar los parámetros de todas las ecuaciones. Puedes modificar el valor de X, Y y Z; en número de divisiones, los puntos de corte y definir la calidad de la representación.
Además de generar y representar funciones gráficamente, Winplot incluye dos funciones adicionales. Un generador de órbitas planetarias para calcular trayectorias de objetos en el espacio y una serie de test que te ayudarán a evaluar tus conocimientos.

Descargar Winplot

*Padowan Graph
Con esta sencilla aplicación podrás dibujar gráficas de funciones matemática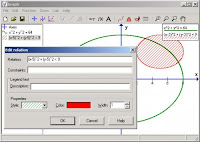s en un sistema de coordenadas, de forma sencilla y precisa. Puedes trabajar tanto con gráficas normales como con funciones de parámetro.
Soporta una amplia variedad de funciones ya integradas (seno, coseno, tangente, logaritmo, raíz cuadrada, factorial...) y las puedes dibujar en diferentes colores y estilos de línea para distinguirlas fácilmente unas de otras, así como añadir sombras y puntos a todo el sistema de coordinadas.
Puedes guardar la función como un archivo gráfico, imprimirla o copiarla y pegarla en otras aplicaciones. Graph también permite realizar algunos cálculos basados en la función representada en la gráfica.

Descargar Padowan Graph

http://www.softonic.com/windows/matematicas

Matemáticas y Publicidad

Esta es una pequeña muestra de como los publicistas utilizan elementos de las matemáticas para señalar las "bondades" de sus productos....

Perfección matemática

Álgebra de la seducción

¡Qué miedo!

Anuncio de un concurso de TVE

Confusión Asociatividad

http://www.catedu.es/matematicas_mundo/index.html

Matemático, la profesión mejor considerada

Un estudio realizado por "The World Street Journal" establece una lista con las 200 mejores profesiones, según diferentes criterios, como proyección profesional, ambiente laboral, salario, exigencia física o nivel de estrés, por citar algunos. Los resultados del estudio, realizado por Les Krant, se basan en datos del departamento estadounidense de Estadísticas del Trabajo. Los diez mejores empleos son los siguientes:
1. Matemático (Aplica teorías matemáticas y ecuaciones para enseñar o resolver problemas).
2. Estadístico en seguros (Interpreta estadísticas para determinar probabilidades de accidentes, enfermedades, desastres naturales, etc.).
3. Estadístico (Tabula, analiza, e interpreta los resultados numéricos de experimentos y estudios).
4. Biólogo.
5. Ingeniero de Software.
6. Analista de Sistemas.
7. Historiador.
8. Sociólogo.
9. Diseñador Industrial.
10. Contable.
El trabajo reconoce así que la profesión de matemático tiene y seguirá teniendo demanda en el mercado de trabajo, entre otras cosas por su versatilidad. Como se explica en el estudio, un matemático puede emplearse en una universidad, en un laboratorio médico, en una productora de cine, o en el sector informático, financiero, farmacéutico, aeroespacial o incluso en aseguradoras. El Departamento del Trabajo de Estados Unidos estima que la demanda de matemáticos subirá en un 10% de aquí a 2016. ¿Y qué ocurre en España? La situación es francamente buena. La Real Sociedad Matemática Española publicó un estudio que muestra que el paro es prácticamente nulo entre los matemáticos. La salida docente (universitaria o en la enseñanza secundaria) ha dejado de ser la única hace ya mucho tiempo.
Ir al artículo en The World Street Journal (en inglés)

La progresión más antigua

El problema de progresiones más antiguo no es el de la recompensa al inventor del ajedrez, que tiene ya más de dos mil años, sino otro mucho más viejo, repartición del pan, registrado en el célebre papiro egipcio de Rind. Este papiro, hallado por Rind a fines del siglo pasado, fue escrito unos 2 000 años antes de nuestra era y constituye una copia de otra obra matemática aún más remota que data seguramente del tercer milenio antes de nuestra era. Entre los problemas aritméticos, algebraicos y geométricos que figuran en dicho documento aparece el que transmitimos en traducción libre.

Entre cinco personas se repartieron cien medidas de trigo, de tal suerte que la segunda recibió más que la primera tanto como le correspondió a la tercera más que a la segunda, a la cuarta más que a la tercera y a la quinta más que a la cuarta. Además, las dos primeras obtuvieron siete veces menos que las tres restantes. ¿Cuánto correspondió a cada una?

Algebra Recreativa Yakov Perelman

Uno mas uno....

Uno mas uno

Publish at Scribd or explore others:

Matemáticas y el fin del mundo. La torre de Brahma

En su libro Uno, dos, tres, infinito... el gran físico George Gamow, cuenta la siguiente historia: “En el templo de Benarés, bajo la cúpula que señala el centro del mundo, hay una placa de latón en la cual se han fijado tres agujas de diamante, cada una de las cuales tiene la altura de un codo (alrededor de cincuenta centímetros). Ensartados en una de estas agujas, el día de la creación, Dios colocó sesenta y cuatro discos de oro puro. El disco más grande se apoya sobre la p laca y los otros disminuyen de diámetro a medida que se acercan a la parte superior. Esta es la torre de Brama. Día y noche, incesantemente, un sacerdote transfiere los discos de una aguja de diamante a la otra, de acuerdo con las leyes de Brahma, fijas e inmutables, que requieren que el sacerdote mueva un solo disco por vez y que nunca coloque un disco menor debajo de otro más grande. Cuando se hayan transferido así los sesenta y cuatro discos de la aguja en la cual Dios los colocó, durante la creación, a una de las otras agujas, la torre, el templo y los Brahmanes se desmenuzarán hasta convertirse en polvo, y en medio de un trueno, el mundo desaparecerá.

El relato muestra que Brama no sólo era un Dios, sino un buen matemático, conocía el rápido crecimiento de las series geométricas y tomó precauciones como para que el mundo durara un lapso razonable. Pero podía haberlo hecho durar muchísimo más sólo con exigir que en vez de cambiar los discos de una aguja a otra, los sacerdotes simplemente se ocuparan de cambiarlos de lugar, ordenándolos de todas las maneras posibles. Los números que miden la cantidad de formas en que se puede ordenar una cierta cantidad de objetos crecen tan fantásticamente que a su lado, 18.446.744.073.709.551.615 apenas cuenta. Para describir la cantidad de formas en que pueden ordenarse sesenta y cuatro discos, hace falta un uno seguido de ochenta y ocho ceros. Si Brama hubiera elegido esta variante y si los sacerdotes hubieran sido capaces de exhibir un ordenamiento por segundo, la duración del mundo en años vendría dada por un cuatro seguido de ochenta y un ceros: los idiomas humanos no tienen palabras para semejantes números. Es una lástima, pero ya sabemos que los dioses suelen jugar con el tiempo, y la eternidad misma para ellos no es nada.

En el año 1883 el matemático francés François Edouard Anatole Lucas, bajo el pseudónimo de PROFESSOR N. CLAUS (DE SIAM) Mandarin of the College of Li-Sou-Stian! presentó un juego basado en esta leyenda al que llamó Torre de Hanoi, en el que utilizaba solamente 8 discos.

Encuentran número primo de casi 13 millones de dígitos

Los números primos están de moda, y cada vez que se “descubre” uno nuevo es noticia. Recordemos que un número primo es aquel mayor que uno, divisible únicamente por si mismo y por la unidad. Como es lógico, cada vez son más grandes, y el caso que mencionamos se lleva el premio gordo. Casi 13 millones de dígitos tiene este número primo encontrado con un simple programa que utiliza casi la misma fracción de memoria que el protector de pantalla de un computador.
Este programa se comunica a través de Internet con el servidor PrimeNet y trata de encontrar números primos de un tipo especial, llamados primos de Mersenne, que son de la forma 2^p-1, donde p es un número primo.
El protagonista es el 2^43,112,609-1, un número de casi 13 millones de dígitos, el cual le hace merecedor del premio de 100.000 dólares que la Fundación de Frontera Electrónica ofrecía al descubridor del primer número primo de al menos 10 millones de dígitos.
El número descubierto también se coloca en el lugar 45 de la lista de los récords de los números primos de Mersenne, establecida hace unos 2.500 años. Dos semanas después se halló el 46º primo de Mersenne (2^37156667 - 1) de casi 11 millones de dígitos pero por poquito, se quedó sin el premio.
El próximo reto es realmente colosal, con un premio de $150,000 dólares por el primer primo que se descubra de 100 millones de dígitos.

http://www.novaciencia.com/category/matematicas/

Origen de los símbolos matemáticos

- El matemático alemán Michael Stifel (1485 -1567) en su obra Arithmetica Integra popularizó los símbolos “+” y “-” desplazando a los signos “p” (plus) y “m” (minus). Según el matemático español Rey Pastor (1888-1962), los signos “+” y “-” fueron utilizados por primera vez por el científico alemán Widmann (1460-1498).
- Robert Recode (1510-1558), matemático y médico inglés, fue el creador del símbolo “=“. Para él no había dos cosas más iguales que dos lineas rectas paralelas.
- El símbolo que conocemos como “raíz de” apareció por primera vez en un libro alemán de álgebra de 1525. Antes, para designar la raíz de un número se escribía literalmente “raíz de …”. Para abreviar se usó simplemente la letra “r“, pero cuando los números eran grandes se alargaba el trazo horizontal de la misma dando origen al símbolo que utilizamos hoy en día.
- El matemático François Viète (1540 - 1603) fue el primero en utilizar letras para designar las incógnitas y constantes.
- A Tomas Harriot (1560 - 1621) le debemos los signos actuales de “>” y “<“, y el “.” como símbolo de multiplicación. - Los símbolos de multiplicación “x” y división “:” fueron introducidos por el matemático William Oughtred (1574-1660) en el año 1657. - El símbolo de la integral fue propuesto por Gottfried Leibniz (1646-1716) y lo extrajo de la palabra latina “summa” tomando su inicial. A Leibniz le debemos muchos más signos notacionales como “dx” y además fue quien popularizó el “.” como signo de multiplicación. Más información: La evolución de los signos aritméticos