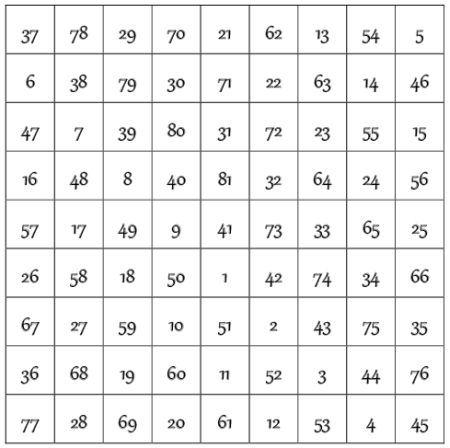
Este ‘grimorio’ fue redactado por el papa León III (750-816) hacia el año 795: era un regalo para el emperador Carlomagno.
En este texto aparece un misterioso cuadro con números –eliminado en ediciones posteriores como la de 1660– sin ningún comentario: es un de orden 9 y de constante mágica –suma común de las cifras de cada una de las 9 filas, de las de las 9 columnas o de los números de las 2 diagonales– 369.
Destacamos debajo algunas de las muchas propiedades aritméticas que posee este enigmático cuadrado:
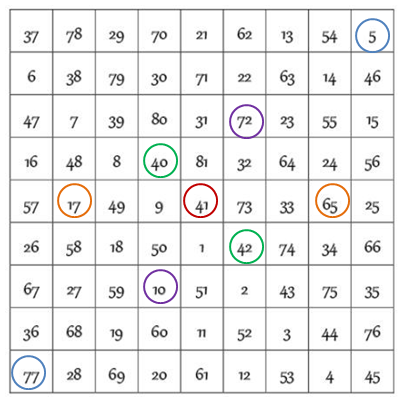
1) La suma de los términos simétricos respecto al centro del cuadrado es constante e igual a 92+1 = 82 –la constante de polarización–, y la casilla central es justo la mitad de esta constante: 41. Debajo se muestra el cuadrado central en rojo y algunas casillas simétricas respecto al centro (marcadas con diferentes colores para apreciar las simetrías y la constante de polarización).
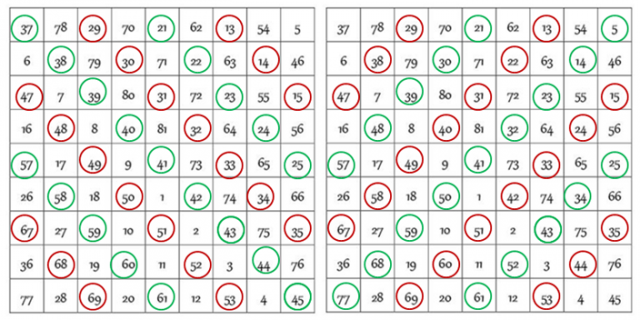
2) Si se observan las diagonales paralelas a la primera diagonal –la que va de la esquina superior izquierda a la esquina inferior derecha–, en una de cada dos sus términos son los de una progresión aritmética de razón 1. Sucede lo mismo para la otra diagonal aunque, en este caso, la progresión geométrica es de razón 9.
3) Se obtiene el número mágico 369 con muchas otras combinaciones de 9 números aparte de las filas, columnas y diagonales (ver [1]).
4) Es un cuadrado autocomplementario, es decir, cuando se reemplaza el número aij(situado en la fila i y la columna j) por el número 92+1–aij, se obtiene otro cuadrado mágico que se llama complementario del primero. En este caso, además, tras rotarlo 180 grados, este último coincide con el cuadrado original (ver [1]).
5) El cuadrado papal está formado por 9 subcuadrados de orden 3, que poseen también sorprendentes propiedades (ver [1]).
En el artículo [1] se explica también un método simple para construir el cuadrado papaly algunas otras propiedades interesantes.
Como muy bien dice el autor, a pesar del origen enigmático de este cuadrado –¿formaría parte quizás de algún oscuro conjuro?–, no hay nada misterioso ni mágico en él: sólo posee propiedades muy interesantes… mucho más que interesantes ¡son realmente extraordinarias!